Fyzikální proces difrakce na periodické struktuře

Složitější (obecné) difrakční struktury je možné vždy rozložit na pravidelné difrakční struktury - difrakční mřížky. Proto je znalost fyzikálního procesu difrakce na takovýchto strukturách důležitá. Difrakční proces na mřížce chápeme jako výsledek interference difraktovaných příspěvků od jednotlivých period mřížky. Vznikají tak difrakční řády, jako projev fázového synchronismu difrakčních příspěvků z plochy mřížky, tedy optimálního načítání všech jednotlivých dílčích vln. Způsob načítání je přitom ovlivněn fází jednotlivých příspěvků, která je dána drahou, kterou jednotlivé příspěvky projdou. Vyšší počet difrakčních řádů je důsledkem opakovatelnosti tohoto synchronismu pro více směrů difraktovaného světla. Podmínka fázového synchronismu difraktovaných příspěvků je dána tzv. mřížkovou rovnicí  

$$\sin\theta_d = \sin\theta_i + m\frac{\lambda}{\Lambda}$$

Rovnice nám udává, na základě jednoduché geometrické představy, pod jakým úhlem ($\theta_d$) se bude světlo ohýbat do příslušného m-tého difrakčního řádu v závislosti na prostorové periodě difrakční mřížky $\Lambda$ a vlnové délce $\lambda$, pokud světlo dopadá na mřížku pod úhlem ($\theta_i$). Mřížková rovnice ale vždy uvažuje pouze buď difrakční řády mřížkou prošlé (transmisní) nebo od mřížky odražené (reflexní). V obecném (a často i reálném) případě je chování mřížky složitější, vznikají jak řády transmisní, tak řády reflexní, jak je znázorněno na Obrázku 7. Pro názornost byl zvolen jeden typ mřížky - binární reliéfní, a jeden typ polarizace dopadající vlny - tzv. TE (příčně elektrická) polarizace - vektor elektrického pole kmitá rovnoběžně s mřížkovými vrypy.

  

Obrázek 7: Difrakce světelného paprsku na periodické difrakční struktuře - mřížce. R značí reflexní řády, T řády transmisní. Řády jsou číslovány od nultých řádů - prošlé a reflektované vlny.

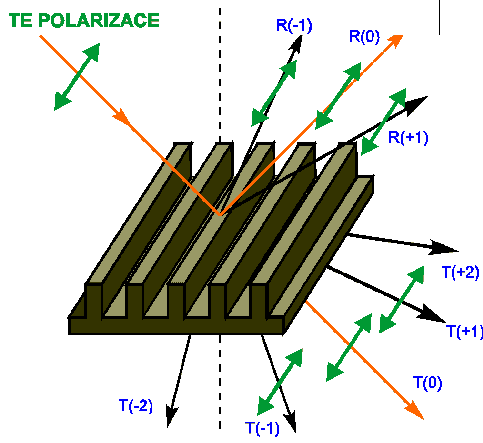
Difrakční struktury se charakterizují pomocí difrakční účinnosti, pomocí které se posuzují vlastnosti a aplikační možnosti. Difrakční účinnost vyjadřuje energetickou účinnost užitečné transformace při difrakci. Difrakční účinnost se definuje pro daný difrakční řád jako poměr výkonu difraktovaného z určité plochy mřížky do daného difrakčního řádu, ku výkonu dopadajícímu na elementární plochu mřížky. Pomocí difrakční účinnosti lze tedy popsat intenzitu v jednotlivých vlnách na Obrázku 7. Rozlišují se dva případy podle odlišného charakteru difrakce.

U velmi tenké mřížky je difrakce procesem neselektivním, tedy probíhá co se týče kvality stejně pro různé vlnové délky a pro různé úhly dopadu vln, pouze se příslušně změní úhel difrakce (podle mřížkové rovnice).

Příklady tenkých mřížek Jako základní příklady tenkých mřížek mohou sloužit mřížky amplitudové a fázové: amplitudová harmonická mřížka (lze dosáhnout maximální difrakční účinnosti v prvním difrakčním řádu 6.25%), amplitudová binární mřížka (účinnost 10%), fázová harmonická mřížka (účinnost 34%), fázová binární mřížka (účinnost 40%).

 Naopak, v případě tlustších mřížek (nazývají se objemové) dochází k načítání příspěvků i z objemu difrakční struktury. Aby se příspěvky co nejvíce načetli (podmínka fázového synchronismu), musí být splněna tzv. Braggova podmínka, která spolu jednoznačně svazuje směry dopadající a difraktované vlny. Splnění této podmínky si lze představit jako odraz světla od rovnoběžných odrazných rovin, přičemž od každé roviny se odrazí pouze část světla a zbytek projde. Pokud jsou roviny od sebe vzdálené o vzdálenost L, pak fáze odražených vln je určena $\varphi = 2k\lambda\sin\theta$, kde $k = 2\pi/\lambda$ je vlnové číslo dopadající vlny ($\lambda$ je vlnová délka) a $\theta$ je úhel, pod kterým světlo dopadá na odrazné roviny. Situace je znázorněna na Obrázku 8. $\vec{K}$ je mřížkový vektor, $\vec{k_i}$ je vlnový vektor vlny dopadající, a $\vec{k_d}$ je vlnový vektor vlny difraktované. Jak je vidět z Obrázku 8, Braggovu podmínku lze zapsat i pomocí vlnových vektorů ve tvaru: $\vec{K} = \vec{k_d} - \vec{k_i}$.

  

Obrázek 8: Difrakce světla na objemové mřížce.

Existuje úhel, pro který je celková intenzita odraženého světla maximální (tzv. Braggův úhel - $\theta_B$): $\sin\theta_B = \lambda/(2\Lambda)$. Při přesném splnění Braggovy podmínky zůstávají na výstupu z mřížky pouze dvě vlny (nultý a první řád). Ostatní difrakční řády zanikají, protože se pro ně příspěvky od jednotlivých vrstev mřížky vzájemně vyruší. Tím je umožněno zvýšení difrakční účinnosti, ale mřížka se také stává selektivní, tj. difrakce je optimální (a často vůbec existuje) pouze pro určitý rozsah vlnových délek dopadajícího světla, a pro určitý rozsah úhlů dopadu. Jako příklad takovýchto objemových struktur mohou sloužit, kromě objemových mřížek vytvořených z materiálů určených pro objemové difrakční struktury také dielektrické vrstvy (vytvářené např. napařováním).

Zpět: Polarizace světla O úroveň výše: Optika a moderni technologie Pokračovat: Fyzikální principy optických prvků