Fyzikální principy optických prvků - korektorů

Základní požadavek, který klademe na optické elementy je schopnost určitým způsobem prostorově "transformovat" světlo. Geometrická optika pod tímto pojmem v podstatě rozumí aplikaci dvou základních zákonů této geometrické optiky: zákona odrazu a lomu. Vlnová optika umožňuje rozšířit tento pohled a vytvořit přesnější představy o tomto pojmu "transformovat" - mluvíme o tzv. optických fázových korektorech. Optickým elementem většinou nazáváme fázový korektor, jehož fázová korekce je relativně jednoduchá a tím i obecná, uplatnitelná pro jakoukoliv vlnoplochu. Např. lineární fázová korekce naklání vlnoplochu (např. hranol, klín), kvadratická fázová korekce může mít fokuzační nebo zobrazovací funkci (čočky, sférická zrcadla). Složitější fázová korekce má smysl jen u definované vstupní vlnoplochy, ze které dělá korektor vlnoplochu požadovanou - např. speciální korekční desky, nebo může představovat vytvoření obrazu z pravidelné vlnoplochy (hologram).

Jestliže z fyzikálního hlediska zvažujeme všechny mechanismy, schopné fázové korekce optické vlnoplochy, je zřejmé, že optické elementy lze konstruovat jako: refrakční (tvarováním lámavého rozhraní dvou prostředí o různých indexech lomu - čočky, hranoly), reflexní (tvarováním odrazného rozhraní - zrcadla rovinná, sférická, asférická), a difrakční (změnou difrakčních linií difrakčního rozhraní - hustoty, tvaru).

Názornou představu o difrakci světla na mřížce lze získat i pomocí tzv. vektorových diagramů vlnových vektorů, což jsou kolmice na vlnoplochy mající velikost $2 \pi n / \lambda$ (n je index lomu daného prostředí a $\lambda$ je vlnová délka světla); v přiblížení geometrické optiky směr tohoto vektoru znamená směr šíření paprsku. 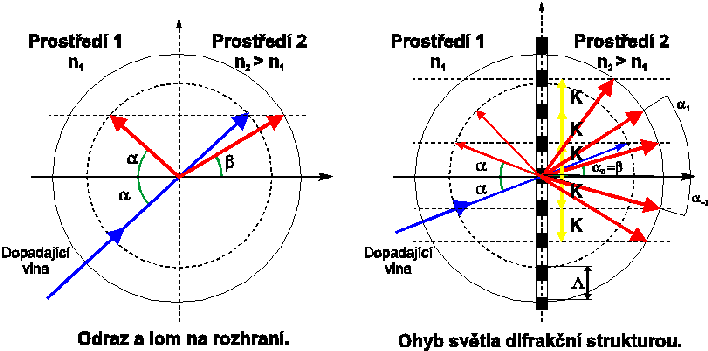Z elektrodynamiky je možno odvodit podmínku, že na rozhraní dvou homogenních prostředí jsou vlnové vektory vlny dopadající a lomené (odražené) nasměrovány tak, že průměty všech těchto vlnových vektorů do roviny rozhraní jsou stejné (podmínka spojitosti vlnových vektorů - okrajová podmínka pro elektrické pole) - viz. levá část Obrázku 9.

  

Obrázek 9: Vektorový diagram vlnových vektorů znázorňující odraz a lom na homogenním rozhraní a na difrakční struktuře.

Při průchodu vlny homogenním (stejnorodým) rozhraním zůstavají průměty vektorů do roviny rozhraní stejné (prostředí 1 - index lomu n₁, prostředím 2 - index lomu n₂ > n₁). Protože odraz nastává do prostředí se stejným indexem lomu jako prostředí původní, zůstávají stejné i úhly dopadu a odrazu. Naopak při lomu dochází k proniknutí záření do prostředí s jiným indexem lomu. Aby byly rovnoběžné složky opět zachovány, musí dojít k našikmení vektoru (jeho délka je dána násobkem indexu lomu), a tudíž se původní úhel $\alpha$ změní na $\beta$ - odtud plyne známý zákon lomu v podobě sinů. Pro využití této transformace se v praxi tvaruje rozhraní, tj. vytváří se obecně zakřivená rozhraní, která jsou schopna provádět požadovanou transformaci. Pro zobrazovací účely se volí povrchy kulové (sférické), v některých případech i asférické. Technologie vytváření je buď broušením a leštěním povrchů, lisováním (zejm. u plastových materiálů), u technologie mikrooptických součástek je popsána dále.

Jestliže je prvek tvořen postupnou změnou indexu lomu (tzv. gradientní prvky), výše řečená podmínka platí v každé diferenciální změně indexu lomu, což vede ke spojitému zakřivení dráhu paprsku, avšak pro stejný gradient (spád indexu lomu) jsou všechny průměty do roviny kolmé na směr gradientu stejné.

Rozhraní nemusí ovšem být homogenní, ale může se periodicky měnit. (s prostorovou periodou $\Lambda$) - obecná difrakční struktura. Periodicita rozhraní si bude vynucovat i stejnou periodicitu mezi vlnami na rozhraní. Ve vektorovém vyjádření je periodicita charakterizována pomocí mřížkového vektoru $\vec{K}$, jehož velikost je rovna $K = 2\pi/\Lambda$. Místo jedné odražené a jedné lomené vlny pak vznikne celý vějíř vln (tzv. difrakční řády) odražených (reflexních) a lomených (transmisních). Jejich směry jsou dány jednak právě periodickou podmínkou na rozhraní, jednak indexy lomu obou prostředí.

Pro takovéto tzv. difrakční rozhraní (pravá část Obrázku 9) s periodicitou mřížky $\Lambda$ a tedy mřížkovým vektorem o velikosti $2 \pi/\Lambda$ plyne z mřížkové rovnice, že oba vlnové vektory, dopadající a difraktovaný, se liší právě o celočíselný násobek mřížkového vektoru.

Na rozdíl od spojitosti fáze na homogenním rozhraní (zákon odrazu a lomu) je u periodických struktur (mřížek) fáze nespojitá, a skok je úměrný mřížkovému vektoru. Fázi je tedy možno měnit pomocí změny hustoty či tvaru difrakčních linií, i když tvar rozhraní zůstane stejné (rovinné). Tohoto se využívá u hologramů nebo difrakčních optických elementů.

Zpět: Fyzikální proces difrakce na O úroveň výše: Optika a moderni technologie Pokračovat: Difrakční struktury a optické