|
|
Úvod do moderní fyziky |
|
Introduction to Modern Physics |
|
| PŘÍKLADY KE KURSU / PROBLEMS TO THE COURSE | |
|
|
Úvod do moderní fyziky |
|
Introduction to Modern Physics |
|
| PŘÍKLADY KE KURSU / PROBLEMS TO THE COURSE | |
Sorry, text of the assignements is until now available only in Czech
| ULH | 1 | 2 | 3 | 4 |
|
ULH 1 |
Jednotky atomové fyziky | První představy moderní fyziky |
| Units in Atomic Physics | First Concepts of Modern Physics | |
|
ULH 2 |
Fotony | De Broglieovy vlny | Koncepce duality mikroobjektů |
| Photons | De Brogglie Waves | Concepts of the Duality of the Microobjects | |
|
ULH 3 |
Stavba atomu | Jednoduché kvantové modely | Vodíkový atom |
| Structure of the Atom | Simple Atomic Models | Hydrogen Atom | |
|
ULH 4 |
Mnohočásticové systémy | Zakladní pojmy fyziky plazmatu | Termojaderná fúze |
| Multiparticle Systems | Fundamental Terms of Plasma Physics | Thermonuclear Fusion |
|
|
|
Jednotky atomové fyziky / Units in Atomic Physics
První představy moderní fyziky | First Concepts of Modern Physics

Úvod | Introduction
Začneme několika (snad) zcela triviálními příklady. Pro řešení samozřejmě stačí obyčejná kalkulačka a tabulky fyzikálních konstant. Některé z příkladů jsou inspirovány úlohami ve skriptu Havránková E.,Janout Z., Štoll I. : Úvod do fyziky v řešených příkladech, Vydavatelství ČVUT, Praha 1998, o němž se tvrdí, že je určeno především pro středoškoláky, kteří chtějí studovat na FJFI. Omlouvám se, jestli se Vás to dotkne, ale pro jistotu to zkuste.
Zadání úloh | Problems
Úloha 1-1
* V atomové fyzice užíváme často jako jednotky
energie (a) 1 elektronvolt (eV) a (b) 1 Rydberg (Ry). Určete ekvivalenty těchto
jednotek v Joulech.
Úloha 1-2
* Energie vazby molekuly vodíku H2 je 4.48 eV. V
chemii se vazebná energie obvykle vyjadřuje v kJ/mol. Jaká je vazebná
energie molekuly vodíku v těchto jednotkách ?
Úloha 1-3
* Při výpočtech nás budou často zajímat počty různých
částic v daném objemu. Určete, kolik je v 1 cm^3 hliníku, zlata a uranu (a)
atomů, (b) elektronů.
Úloha 1-4
* Elektron má kinetickou energii 10 MeV. Určete (a)
jeho hybnost a (b) rychlost.
Úloha 1-5
* Proton se pohybuje rychlostí v = 0.86c, kde c je
rychlost světla. Určete hybnost této částice v jednotkách MeV/c.
Úloha 1-6
* Při střední vzdálenosti Země od Slunce 1.5x10^11
m je hustota radiační energie (sluneční konstanta) 1.4x10^3 W/m 2. Určete
rychlost (v kg/s) s níž klesá hmotnost Slunce v důsledku emise této energie.
Úloha 1-7
* Uvažujeme foton o energii 1 eV. Určete (a)
frekvenci, (b) vlnovou délku, (c) vlnočet odpovídajícího záření
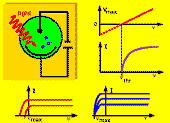 Pro zobrazení v plné velikosti klikněte na obrázek.
Pro zobrazení v plné velikosti klikněte na obrázek.
Úloha 1-8
* Na povrch kovu dopadá ve vakuu záření o vlnové délce
600 nm. Z kovu uvolněné elektrony mají energii 0.5 eV. Jaká je maximální
vlnová délka záření, které může u tohoto kovu vyvolat ještě fotoefekt
?
Úloha 1-9
* Laser generuje záření s hustotou zářívého toku
3x10^17 W/m^2. Sluneční konstanta je 1.4x10^3 W/m^2. Určete (a) tlak záření
generovaného tímto laserem, (b) poměr tohoto tlaku k tlaku slunečního záření.
Úloha 1-10
* Současné subpikosekundové lasery jsou schopny
generovat po fokuzaci záření s hustotou zářivého toku až 10^20 W/cm^2.
(a) Určete počet fotonů záření o vlnové délce 0.5 nm dopadajících při
této hustotě toku na plochu o poloměru 5 mikronů.
Fotony | Photons
De Broglieovy vlny | De Broglie Waves
Koncepce duality mikroobjektů | Concepts of the Duality of the Microobjects

Úvod | Introduction
Doufáme, že tentokrát jsou úlohy zajímavější, než jednoduché problémy zadané v "zahřívacím kole". Některé úlohy vedle vyčíslení vzorců potřebují provést též pár analytických výpočtů, ty jsou však tak jednoduché, že se dají lehce zvládnout.Informace k oddílu fyziky, k němuž se úlohy vztahují, najdete např. v knize Beiser A. : Úvod do moderní fyziky. Academia, Praha 1987.
Zadání úloh | Problems
Úloha 2-1
* Lidské oko má největší citlivost v okolí vlnové
délky 500 nm. (a) Při jaké teplotě černého tělesa bude maximum spektra
emitovaného záření mít tuto vlnovou délku. (b) Srovnejte zjištěnou
hodnotu s teplotou povrchu Slunce.
Úloha 2-2
* Pro teplotu tzv. reliktního záření Vesmíru se udává
hodnota 2.7 K. Určete, pro jakou (a) vlnovou délku, (b) frekvenci má radiance
tohoto záření maximum.
Úloha 2-3
* Určete teplotu povrchu Země za předpokladu, že
povrch naší planety se chová jako černé těleso a jediný zdroj energie, jež
ji ohřívá, je Slunce.
Úloha 2-4
* Rentgenové záření o vlnové délce 10^-11 m je
rozptylováno na terčíku. (a) Určete vlnovou délku záření rozptýleného
pod úhlem 30 stupňů. (b) Určete maximální vlnovou délku rozptýleného záření.
určete maximální kinetickou energii odražených elektronů.
Úloha 2-5
* V rentgence se používá urychlovací napětí 50
kV. Určete (a) nejkratší vlnovou délku záření emitovaného touto
rentgenkou, (b) frekvenci a (c) vlnočet tohoto záření.
Úloha 2-6
* Ukažte, že přeměna fotonu na elektronový pár
nemůže probíhat bez přítomnosti další částice. ( Rada : Uvažte, že v
systému musí platit zákony zachováním energie a hybnosti.)
Úloha 2-7
* Foton červeného světla o frekvenci 7.4Ex10^-14
s^-1 se pohybuje ("padá") v zemském gravitační poli ve svislém směru
na dráze o délce 22.5 m . Jak se změní frekvence odpovídajícího záření
na této dráze ?

Úloha 2-8
* Elektrom byl urychlen napětím 100 V. (a) Určete
vlnovou délku elektronu přiřazené de Broglieovy vlny. (b) Jakým napětím
by elektron musel být urychlen, aby minimální vlnová délka jím generovaného
rentgenového záření byla stejná ?
Úloha 2-9
Určete vlnovou délku de Broglieovy vlny pro následující
případy : (1) Prachová částice o hmotnosti 1x10^-9 g a rychlosti 1 cm/s.
(2) Elektron o kinetické energii 1 eV. (3) Elektron o kinetické energii 100
MeV.
Úloha 2-10
* Uvažujeme elektron, jemuž přísluší délka de
Brogliovy vlny 2 pm. Určete (1) kinetickou energii, (b) fázovou rychlost a (c)
grupovou rychlost této vlny.
Úloha 2-11
*Jaké urychlovací napětí by mělo být použito v
elektronovém nikroskopu, aby bylo možné rozlišit (a) virus o průměru 12
nm, (b) atom o poloměru 0.12 nm, (c) proton o průměru 12 fm ?
Úloha 2-12
Atomy plynu mohou být popisovány jako klasické částice
jestli jim přiřazená délka de Brogliovy vlny je mnohem menší než jejich
střední vzdálenost. (a) Ověřte, zda je tato podmínka splněna pro plyn o
tlaku 1x10^5 Pa a teplotě 300 K. (b) Při jaké hustotě při stejné teplotě
už tato podmínka splněna nebude ? Při jaké teplotě při stejné hustotě
tato podmínka rovněž nebude splněna ?
Stavba atomu | Structure of the Atom
Jednoduché kvantové modely | Simple Atomic Models
Vodíkový atom | Hydrogen Atom
Úvod | Introduction
Tentokrát se podíváme na pár jednoduchých příkladů ke stavbě atomu a numericky "prozkoumáme" některé nejjednoduší kvantové modely. Pár úloh se týká specielně vodíkového atomu. Všechny příklady jsou asi až moc lehké, ale jeden nikdy neví ... Pro řešení úloh k elementárním kvantovým modelům může bý užitečné skriptum Murla M., Pekárek S. : Fyzika II : Semináře. Vydavatelství ČVUT, Praha 1997.Ten počítač asi potřebovat nebudete, jen snad kdybyste si našli v kapse nebo na Webu vědeckou kalkulačku.

Zadání úloh | Problems
Úloha 3-1
* Částice alfa o energii 5 MeV se při rozptylu na jádře
atomu zlata vychýlila o úhel 10 stupňů. (a) Jak je velký srážkový
parametr pro tuto částici ? Jak by se tento parametr změnil pro odchylku 30
stupňu ?
Úloha 3-2
* Uvažujeme elektron ve vodíkovém atomu v kvantových
stavech n = 1 a n = 2. (a) Jaká je frekvence pohybu elektronu na odpovídajících
kruhových drahách ? Jaká bude frekvence záření emitovaného při přechodu
elektronu ze stavu n = 2 do stavu n = 1 a v jaké je tato frekvence relaci k
frekvencím vypočteným v (a) ?
Úloha 3-3
* Elektron je zachycen v pravoúhlé, nekonečně
hluboké jámě o šířce 1.0x10^-10 m (= řádově rozměr atomu). Jaká
energie v Joulech a eV je zapotřebí pro vybuzení elektronu ze základního do
prvního excitovaného stavu ? Jak lze určit střední hodnotu polohové souřadnice
elektronu <x> ? Jak se liší tato hodnota pro různé kvantové stavy
systému ?
Úloha 3-4
* Elektron se nachází v pravoúhlé, nekonečně
hluboké potenciálové jámě o šířce 0.132 nm a je vybuzen do kvantového
stavu n = 10. (a) Jaká je energie elektronu v eV ? (b) Jaká je neučitost v určení
hybnosti elektronu ? (c) Jak se změní tato neurčitost pro n -> nekonečno
?
Úloha 3-5
* Rozměr atomového jádra je řádu 1.0x10^-14 m. Jaká
by byla energie elektronu v základním stavu nacházejícího se v této
oblasti ? (b) Jakého řádu by byla jeho energie v jámě o šířce odpovídající
velikosti atomu ?
 Pro zobrazení v plné velikosti klikněte na obrázek.
Pro zobrazení v plné velikosti klikněte na obrázek.
Úloha 3-6
* Základní stav elektronu v poli lineárního oscilátoru
je 1.24 eV. Jakou energii je třeba vynaložit, aby se elektron dostal do
kvantového stavu n = 2 ? (b) Jak velká bude hodnota této energie pro kvantový
stav n = 4 ?
Úloha 3-7
* Elektron o energii 0.4 eV dopadá na pravoúhlou
potenciálovou bariéru o výšce 3 eV a šířce 0.1 nm. Jaká je pravděpodobnost
průniku elektronu bariérou ? Jak se změní tato hodnota pro dvojnásobnou šířku
bariéry ?
Úloha 3-8
* Svazek elektronů dopadá na bariéru o výšce 6 eV
a šířce 0.2 nm.Jakou energii musí mít tyto elektrony, aby bariérou
proniklo 1 % z jejich celkového počtu ?
Úloha 3-9
* Elektron vybudil při nepružné srážce vodíkový
atom, jenž byl původně v základním stavu, do stavu n = 3. Jaká energie
byla předána vodíkovému atomu ?
Úloha 3-10
* Berylium je prvek s atomovým číslem Z = 4. Jaké
jsou dvě největší vlnové délky Balmerovy série pro třikrát ionizované
berylium ? V jaké spektrální oblasti toto záření bude ?
Úloha 3-11
* Vodíkové atomy mohou být v laboratorních
experimentech vybuzeny do velmi vysokých kvantových stavů. (a) Do jakého
kvantového stavu byl vybuzen vodíkový atom, jehož poloměr je 0.01 mm ? (b)
Jaká je energie vodíkového atomu v tomto stavu ?
Úloha 3-12
* V tzv. mionovém atomu je elektron nahrazen těžší
částicí, t.zv. mionem o hmotnosti 207 x hmotnost elektronu. (a) Jaká je
nejkratší vlnová délka Lymanovy série pro mionický atom vodíku ? (b) Čemu
se rovná poloměr prvního Bohrova orbitu pro pro mionický atom olova (Z = 82)
?
Mnohočásticové systémy | Multiparticle Systems
Základní pojmy fyziky plazmatu | Fundamental Terms of Plasma Physics
Termojaderná fúze | Thermonuclear Fusion
Úvod | Introduction
V tomto oddílu si spočítáme pár zcela jednoduchých příkladů z kinetické teorie a elementární fyziky plazmatu. Pokud jste nebyli na přednášce, doporučujeme se podívat do první kapitoly knihy Chen F. : Úvod do fyziky plazmatu. Academia, Praha 1984.
Zadání úloh | Problems
Úloha 4-1
* Vzduch je v zásadě směsí molekul dusíku a kyslíku.
Jaká je střední rychlost molekul dusíku a kyslíku vzduchu při teplotě 300
K ?
Úloha 4-2
* Teplota vzduchu ve výšce 80 km je -74 stupňu C.
Jaká je střední rychlost molekul vodíku a dusíku v těchto podmínkách ?
(b) Jaký je poměr těchto rychlostí k únikové rychlosti v této výšce ?
Úloha 4-3
* Vysokoteplotní štěpný jaderný reaktor pracuje při
teplotě 1000 K. Předpokládáme, že neutrony v reaktoru mají stejnou teplotu.
Jaká je jejich střední energie a rychlost ?
Úloha 4-4
* Stanovte hodnotu Debyeovy délky pro elektrony a počty
elektromů v Debyeově sféře pro následující případy : Typická ionosfére
: Elektronová hustota n = 10^11 m^-3 , elektronová teplota KT = 0.05 eV. (b)
Typický plamen : n = 10^14 m^-3, KT = 0.05 eV. (c) Doutnavý výboj : n = 10^16
m -3, KT = 2 eV.
Úloha 4-5
* Porovnejte Debyeovy délky pro následující případy
vysokoteplotního plazmatu : (a) Pinčový výboj : Elektronová hustota n =
10^23 m^-3, elektronová teplota KT = 1000 eV. (b) Laboratorní plazma generované
laserem : n = 10^27 m^-3, KT = 300 eV. (c) Plazma v termonukleárním reaktoru
na bázi tokamaku : n = 10^21 m^-3, KT = 10 keV.
Úloha 4-6
* Doutnavý výboj v trubici o průměru 0.02 m je
charakterizován elektronovou hustotou n = 10^15 m^-3 a teplotou T = 1.5 eV. Lze
stav látky ve výboji považovat za plazma ?
Úloha 4-7
* Termonukleární vodíkové plazma má iontovou
teplotu KTi = 20 keV, jeho elektronová teplota KTe = KTi, jeho iontová
koncentrace ni = 10^21 m^-3, elektronová koncentrace ne = ni. Jak je velký
tlak tohoto plazmatu ?
Úloha 4-8
* Předpokládejme, že se pomocí vysokovýkonného
laseru podařilo vytvořit plně ionizované hliníkové plazma o hustotě 20 g
cm -3 a teplotě 1 keV. Určete (a) elektronovou hustotu, (b) Debyeovu délku,
(c) střední vzdálenost mezi ionty tohoto plazmatu.
