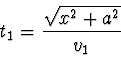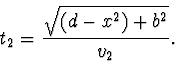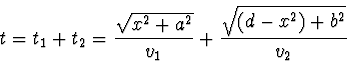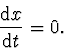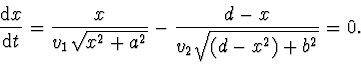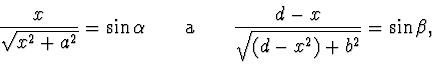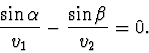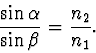![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.5.4 Průchod světelného paprsku
O úroveň výše: 2.5.4 Průchod světelného paprsku
Pokračovat: 2.5.5 Zobrazování tenkou spojnou
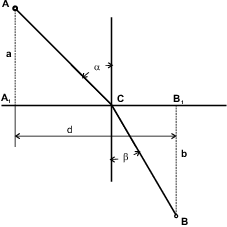
Předpokládejme, že světelný paprsek bude postupovat cestou 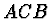 (viz obr.), kde
(viz obr.), kde 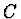 je bod ležící na společném rozhraní obou prostředí.
Když si tento bod zvolíme za začátek pravoúhlého souřadnicového
systému s osou
je bod ležící na společném rozhraní obou prostředí.
Když si tento bod zvolíme za začátek pravoúhlého souřadnicového
systému s osou 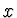 v rozhraní, bod
v rozhraní, bod 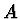 bude mít souřadnici
bude mít souřadnici 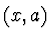 a
bod
a
bod 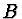 bude mít souřadnici
bude mít souřadnici 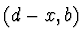 , když jsme vzdálenost paty
kolmice
, když jsme vzdálenost paty
kolmice 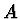 a
a 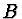 , tj. vzdálenost
, tj. vzdálenost 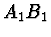 , označili
, označili 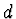 .
.
Když rychlosti světla v jednotlivých prostředích jsou 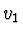 a
a 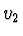 , čas potřebný na proběhnutí dráhy
, čas potřebný na proběhnutí dráhy 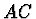 je daný vztahem
je daný vztahem
a čas potřebný na proběhnutí dráhy 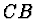 vztahem
vztahem
Celkový čas
má být minimální, co bude splněné, když
Po příslušné derivaci máme:
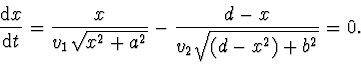 |
(2.61) |
Dále platí:
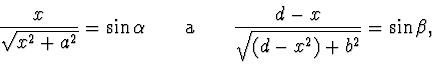 |
(2.62) |
kde 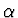 , popř.
, popř. 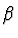 představují úhly, pod kterými světelný
paprsek dopadá na rozhraní, popř. se na něm láme. Po dosazení vztahu
(9) do rovnice (8) dostáváme:
představují úhly, pod kterými světelný
paprsek dopadá na rozhraní, popř. se na něm láme. Po dosazení vztahu
(9) do rovnice (8) dostáváme:
odkud
čili
To je známý zákon lomu. Světlo při přechodu z jednoho prostředí do
druhého vykoná v nejkratším čase dráhu splňující podmínky zákona lomu,
což je ve shodě s Fermatovým principem o šíření optického paprsku mezi
dvěma body 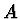 a
a  .
.
![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.5.4 Průchod světelného paprsku
O úroveň výše: 2.5.4 Průchod světelného paprsku
Pokračovat: 2.5.5 Zobrazování tenkou spojnou
Milan Šiňor
2000-02-17

![]() (viz obr.), kde
(viz obr.), kde ![]() je bod ležící na společném rozhraní obou prostředí.
Když si tento bod zvolíme za začátek pravoúhlého souřadnicového
systému s osou
je bod ležící na společném rozhraní obou prostředí.
Když si tento bod zvolíme za začátek pravoúhlého souřadnicového
systému s osou ![]() v rozhraní, bod
v rozhraní, bod ![]() bude mít souřadnici
bude mít souřadnici ![]() a
bod
a
bod ![]() bude mít souřadnici
bude mít souřadnici ![]() , když jsme vzdálenost paty
kolmice
, když jsme vzdálenost paty
kolmice ![]() a
a ![]() , tj. vzdálenost
, tj. vzdálenost ![]() , označili
, označili ![]() .
.
![]() a
a ![]() , čas potřebný na proběhnutí dráhy
, čas potřebný na proběhnutí dráhy ![]() je daný vztahem
je daný vztahem