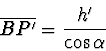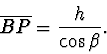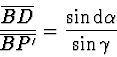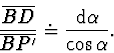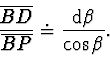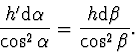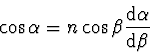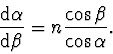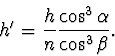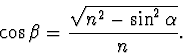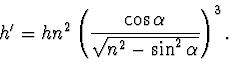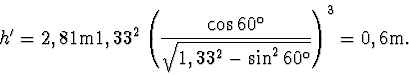![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.5.1 Předmět v bazénu
O úroveň výše: 2.5.1 Předmět v bazénu
Pokračovat: 2.5.2 Rotující rovinné zrcadlo
Vyberme ze svazku paprsků, které vycházejí z předmětu 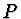 a po lomu na
rozhraní vody a vzduchu vstupují do oka, dva paprsky (1) a (2), které
svírají nepatrný úhel
a po lomu na
rozhraní vody a vzduchu vstupují do oka, dva paprsky (1) a (2), které
svírají nepatrný úhel
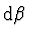 . Lomené paprsky (1') a
(2'), dopadající do oka ze zdánlivého obrazu
. Lomené paprsky (1') a
(2'), dopadající do oka ze zdánlivého obrazu 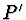 , svírají úhel
, svírají úhel
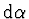 .
.
Podle označení platí:
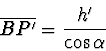 |
(2.54) |
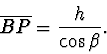 |
(2.55) |
V trojúhelníku 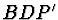 podle sinové věty platí:
podle sinové věty platí:
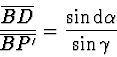 |
(2.56) |
a protože
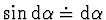 ,
,
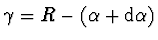 a
a
![$\sin \gamma = \sin [R -(\alpha +
\mathrm {d} \alpha)] = \cos(\alpha + \mathrm {d} \alpha) \doteq \cos
\alpha$](img598.gif) , je možno rovnici (3) přepsat do tvaru
, je možno rovnici (3) přepsat do tvaru
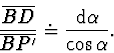 |
(2.57) |
Analogickým postupem z trojúhelníku 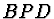 vyplývá:
vyplývá:
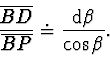 |
(2.58) |
Když vydělíme rovnice (4) a (5) a výsledek porovnáme s výrazem
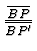 , vyplývajícím z rovnic (1) a (2),
dostaneme vztah
, vyplývajícím z rovnic (1) a (2),
dostaneme vztah
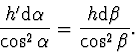 |
(2.59) |
Podíl
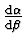 určíme ze
zákona lomu. Derivováním rovnice
určíme ze
zákona lomu. Derivováním rovnice
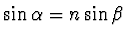 podle
úhlu
podle
úhlu 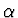 dostáváme:
dostáváme:
odkud
Po dosazení tohoto výrazu do rovnice (6) dostáváme pro zdánlivou
hloubku vztah
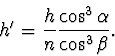 |
(2.60) |
Neznámý úhel 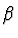 určíme ze zákona lomu
určíme ze zákona lomu
odkud po úpravě dostaneme:
Pro zdánlivou hloubku 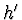 ze vztahu (7) potom vyplývá:
ze vztahu (7) potom vyplývá:
Po dosazení číselných hodnot dostáváme:
V následujícím apletu Bazén
lze volit úhel pozorovaní předmětu.
![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.5.1 Předmět v bazénu
O úroveň výše: 2.5.1 Předmět v bazénu
Pokračovat: 2.5.2 Rotující rovinné zrcadlo
Milan Šiňor
2000-02-17
![]() a po lomu na
rozhraní vody a vzduchu vstupují do oka, dva paprsky (1) a (2), které
svírají nepatrný úhel
a po lomu na
rozhraní vody a vzduchu vstupují do oka, dva paprsky (1) a (2), které
svírají nepatrný úhel
![]() . Lomené paprsky (1') a
(2'), dopadající do oka ze zdánlivého obrazu
. Lomené paprsky (1') a
(2'), dopadající do oka ze zdánlivého obrazu ![]() , svírají úhel
, svírají úhel
![]() .
.