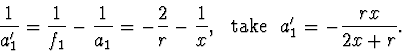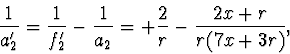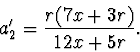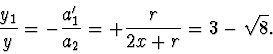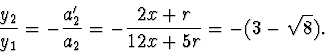Předmět 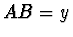 , jenž je ve vzdálenosti
, jenž je ve vzdálenosti 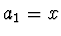 od počátku
(viz. obr. 5), zobrazíme nejprve vypuklým zrcadlem a obraz
od počátku
(viz. obr. 5), zobrazíme nejprve vypuklým zrcadlem a obraz
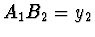 , jím vytvořený, zobrazíme znovu zrcadlem dutým, takže
vznikne obraz
, jím vytvořený, zobrazíme znovu zrcadlem dutým, takže
vznikne obraz 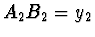 , který se podle zadání
musí nacházet v téže vzdálenosti od zrcadel jako předmět.
, který se podle zadání
musí nacházet v téže vzdálenosti od zrcadel jako předmět.
 |
|
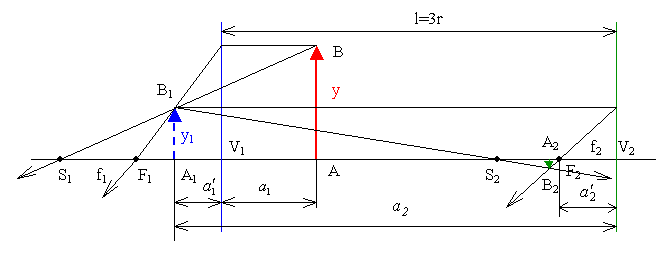
| Obr. 5 |
|
Z vrcholové rovnice vypuklého zrcadla plyne (pro zdánlivý obraz
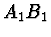 )
)
Zdánlivý obraz 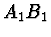 je pro duté zrcadlo předmětem, jehož
vzdálenost od vrcholu dutého zrcadla je
je pro duté zrcadlo předmětem, jehož
vzdálenost od vrcholu dutého zrcadla je
Vrcholová rovnice dutého zrcadla dá pro vzdálenost 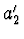 dalšího
obrazu
dalšího
obrazu 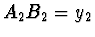 vztah
vztah
z něhož
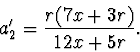 |
(2.42) |
Má-li být splněna podmínka zadání, že 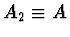 , musí být
, musí být
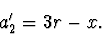 |
(2.43) |
Z rovnosti vztahů (18) a (19) dostaneme po úpravě kvadratickou rovnici
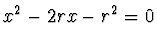 , jejíž kořeny jsou
, jejíž kořeny jsou
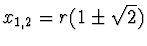 .
Záporný kořen nemá fyzikální význam, neboť předmět by se octl v místě
nepřípustném zobrazení. Předmět tedy musí být od vypuklého zrcadla
vzdálen o délku
.
Záporný kořen nemá fyzikální význam, neboť předmět by se octl v místě
nepřípustném zobrazení. Předmět tedy musí být od vypuklého zrcadla
vzdálen o délku
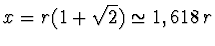 .
.

![]() )
)