![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.4.1 Zobrazení ze skleněné
O úroveň výše: 2.4.1 Zobrazení ze skleněné
Pokračovat: 2.4.2 Pozorování Měsíce hvězdářským
- a)
- Při pozorování mince z pravé strany můžeme pomocí (1) a (2)
pro zvětšení
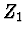 psát (1. případ)
psát (1. případ)
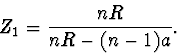 |
(2.27) |
Při pozorování mince z levé strany bude předmětová vzdálenost 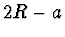 ,
a zvětšení
,
a zvětšení 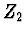 (2. případ)
(2. případ)
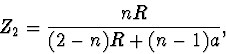 |
(2.28) |
kde 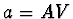 , tj. předmětová vzdálenost mince v prvním případě.
Podíl
, tj. předmětová vzdálenost mince v prvním případě.
Podíl
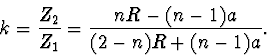 |
(2.29) |
Můžeme se přesvědčit, že 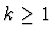 , protože
, protože 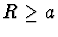 .
.
- b)
- Funkci
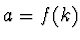 vyjádříme z (5):
vyjádříme z (5):
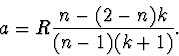 |
(2.30) |
- c)
- Skutečný průměr mince
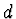 lze určit např. z (3):
lze určit např. z (3):
kde jsme za 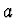 dosadili vztah (6).
Hodnotu
dosadili vztah (6).
Hodnotu 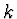 v našem případě můžeme určit ze vztahu (5),
když uvážíme, že
v našem případě můžeme určit ze vztahu (5),
když uvážíme, že 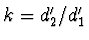 . Potom
. Potom
Výsledek: 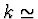 1,86,
1,86, 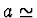 0,399R,
0,399R, 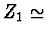 1,15,
1,15,
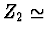 2,14,
2,14, 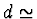 16mm.
16mm.
![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.4.1 Zobrazení ze skleněné
O úroveň výše: 2.4.1 Zobrazení ze skleněné
Pokračovat: 2.4.2 Pozorování Měsíce hvězdářským
Milan Šiňor
2000-02-17
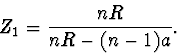
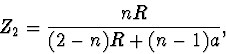
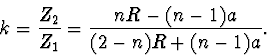
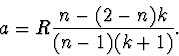
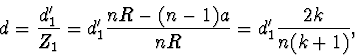
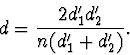
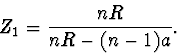
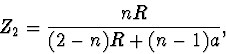
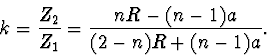
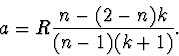
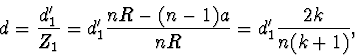
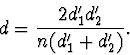
![]() 1,86,
1,86, ![]() 0,399R,
0,399R, ![]() 1,15,
1,15,
![]() 2,14,
2,14, ![]() 16mm.
16mm.