Zadání:
Uvnitř velké koule o poloměru ![]() , zhotovené ze skla o indexu lomu
, zhotovené ze skla o indexu lomu ![]() je umístěná desetihaléřová mince tak, že kolmice k minci sestrojená
z jejího středu splývá s průměrem koule. Jestliže koulí otáčíme proti
světlu, můžeme pozorovat dva optické obrazy mince kruhového tvaru,
a to jeden s minimálním a druhý s maximálním průměrem.
je umístěná desetihaléřová mince tak, že kolmice k minci sestrojená
z jejího středu splývá s průměrem koule. Jestliže koulí otáčíme proti
světlu, můžeme pozorovat dva optické obrazy mince kruhového tvaru,
a to jeden s minimálním a druhý s maximálním průměrem.
Úlohu řešte nejprve obecně, pak pro hodnoty: ![]() 1,50,
1,50,
![]() 18,4mm,
18,4mm, ![]() 34,2mm.
34,2mm.
Předpoklad: Mince ve srovnání s koulí je malá a proto můžeme použít zákony zobrazování paraxiální optiky.
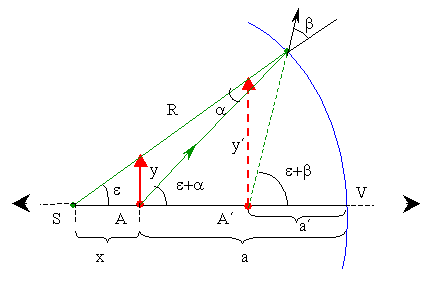 |
| Obr. 1 |
Návod: Odvodíme nejprve zobrazovací rovnici
pro zobrazení bodů z vnitřku skleněné koule
do vnějšího prostoru (obr. 1).
Pro malé úhly ![]() ,
, ![]() a
a ![]() můžeme psát
můžeme psát
| (2.25) |
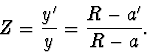
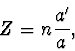 |
(2.26) |