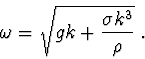2.3.6.1 Řešení

Disperzní relaci budeme hledat ve tvaru . Rozměry proto budou splňovat vztah

$${\rm s}^{-1} = {\rm m}^{-\alpha} {\rm kg}^\beta {\rm m}^{-3\beta} {\rm m}^\gamma {\rm s}^{-2\gamma}$$

Mocniny u kg, m a s se musí shodovat. Odsud dostaneme soustavu tří rovnic:

$$\begin{array}{rl} {\rm kg:} & 0 = \beta\ ,\\ {\rm m:} & 0 = ... ... \beta + \gamma\ ,\\ {\rm s:} & -1 = -2 \gamma,\\ \end{array}$$

která má řešení .

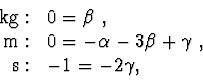
Výsledek: . Vztah jsme obdrželi z rozměrové analýzy a proto by před odmocninou mohl být jakýkoli bezrozměrný multiplikativní koeficient (proto symbol ). Ve skutečnosti je odvozený výraz pro dlouhé vlny správný. Povšimněte si, že výsledek nezávisí na hustotě.

Poznámka: Disperzní relace krátkých vln na hluboké vlně závisí na povrchovém napětí vody, disperzní relace s dlouhovlnnou i krátkovlnnou částí je:

$$\omega = \sqrt{gk + \frac{\sigma k^3}{\rho}}\ .$$