po dosazení a úpravě dostaneme
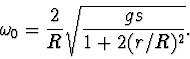 |
(2.8) |
dosazením
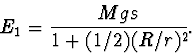
Jaké další druhy energie určíme? Určíme energii
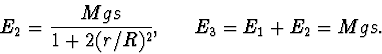
Požadované podíly jsou
![\begin{displaymath}
p_1=\frac{E_1}{E_2}=2\left(\frac{r}{R}\right)^2,~~~~p_2=
\fr...
...{E_3} =\left(1+\frac12\left(\frac{R}{r}\right)^2
\right]^{-1}.
\end{displaymath}](img152.gif)
určíme
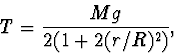
kde za
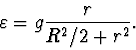
Pro dané hodnoty
Z toho určíme
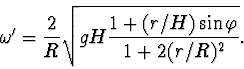 |
(2.9) |
kde
V případě ![]() se výraz (9) zjednoduší. Pak veličina
se výraz (9) zjednoduší. Pak veličina ![]() není funkcí úhlu
není funkcí úhlu ![]() a
a
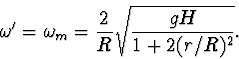
Pro pohyb disku dolů platí
Pro pohyb nahoru máme
kde
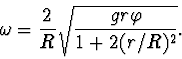
Tato změna nastane za dobu přibližně
Přitom vlákno napíná síla velikosti
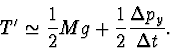
Po dosazení a úpravě dostaneme
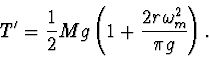
Podmínka, aby nastalo přetržení vlákna, je
![\begin{displaymath}
s<s_m=\frac{\pi r}{4}\left(\frac{2T_m}{Mg}-1\right) \left[1+
\frac12 \left(\frac{R}{r}\right)^2\right].
\end{displaymath}](img182.gif)