![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.1.4.1 Řešení
O úroveň výše: 2.1 Kmity
Pokračovat: 2.1.5.1 Řešení
Zadání: Homogenní válcový disk o hmotnosti 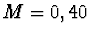 kg,
poloměru
kg,
poloměru 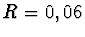 m, tloušťky
m, tloušťky 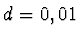 m je zavěšený na dvou
vláknech o stejné délce, která jsou upevněná na hřídeli disku
s poloměrem
m je zavěšený na dvou
vláknech o stejné délce, která jsou upevněná na hřídeli disku
s poloměrem 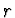 . Vlákna jsou dokonale pevná a dokonale ohebná, jejich
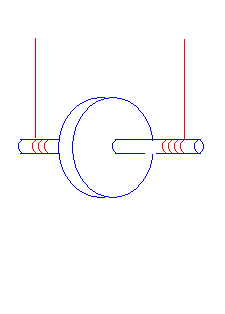
hmotnost a tloušťka je velmi malá (obr. 7). Vlákna navineme na hřídel
disku tak, že těžiště disku se dostane do výšky
. Vlákna jsou dokonale pevná a dokonale ohebná, jejich
hmotnost a tloušťka je velmi malá (obr. 7). Vlákna navineme na hřídel
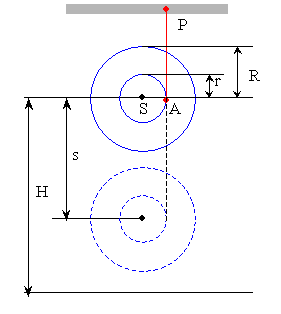
disku tak, že těžiště disku se dostane do výšky 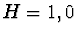 m, kterou
budeme považovat za počáteční polohu (obr. 8).
Potom disk uvolníme. Po dosažení nejnižší polohy začne disk opět
vystupovat nahoru.
m, kterou
budeme považovat za počáteční polohu (obr. 8).
Potom disk uvolníme. Po dosažení nejnižší polohy začne disk opět
vystupovat nahoru.
Řešte následující úlohy:
- a)
- Určete velikost úhlové rychlosti disku
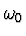 v okamžiku, ve kterém těžiště disku prošlo dráhu (
v okamžiku, ve kterém těžiště disku prošlo dráhu (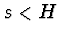 ) od svojí
nejvyšší polohy (obr. 8).
) od svojí
nejvyšší polohy (obr. 8).
- b)
- Určete kinetickou energii
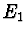 translačního pohybu disku
v okamžiku, ve kterém
translačního pohybu disku
v okamžiku, ve kterém 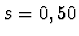 m. Stanovte podíly energie
m. Stanovte podíly energie 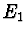 a
jiných možných energií
a
jiných možných energií 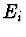 disku v tomto okamžiku, jestliže
poloměr hřídele
disku v tomto okamžiku, jestliže
poloměr hřídele 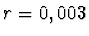 m.
m.
- c)
- Určete tahovou sílu
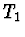 v každém vlákně během klesání
disku.
v každém vlákně během klesání
disku.
- d)
- Vypočítejte velikost úhlové rychlosti
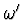 disku při
jeho otáčení v nejnižší poloze, jako funkci úhlu jeho otáčení
disku při
jeho otáčení v nejnižší poloze, jako funkci úhlu jeho otáčení
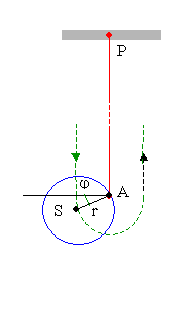
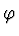 (obr. 9). Určete kvalitativně souřadnice dráhy a
rychlosti těžiště disku ve vhodné souřadnicové soustavě spojené
s okolím, jako funkci úhlu
(obr. 9). Určete kvalitativně souřadnice dráhy a
rychlosti těžiště disku ve vhodné souřadnicové soustavě spojené
s okolím, jako funkci úhlu 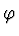 při pohybu disku dolů od bodu
při pohybu disku dolů od bodu
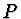 a nahoru k bodu
a nahoru k bodu 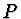 .
.
- e)
- Tahová síla, při které se vlákno přetrhne je
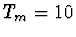 N.
Jaká by měla být dráha klesání disku
N.
Jaká by měla být dráha klesání disku 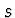 aby se vlákno v bodě obratu
nepřetrhlo?
aby se vlákno v bodě obratu
nepřetrhlo?
Předpoklad:
Při řešení úlohy předpokládejte, že bod 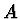 v průběhu
pohybu disku se trvale nachází pod bodem
v průběhu
pohybu disku se trvale nachází pod bodem 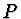 (obr. 8).
(obr. 8).
Subsections
![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.1.4.1 Řešení
O úroveň výše: 2.1 Kmity
Pokračovat: 2.1.5.1 Řešení
Milan Šiňor
2000-02-17
![]() kg,
poloměru
kg,
poloměru ![]() m, tloušťky
m, tloušťky ![]() m je zavěšený na dvou
vláknech o stejné délce, která jsou upevněná na hřídeli disku
s poloměrem
m je zavěšený na dvou
vláknech o stejné délce, která jsou upevněná na hřídeli disku
s poloměrem ![]() . Vlákna jsou dokonale pevná a dokonale ohebná, jejich
hmotnost a tloušťka je velmi malá (obr. 7). Vlákna navineme na hřídel
disku tak, že těžiště disku se dostane do výšky
. Vlákna jsou dokonale pevná a dokonale ohebná, jejich
hmotnost a tloušťka je velmi malá (obr. 7). Vlákna navineme na hřídel
disku tak, že těžiště disku se dostane do výšky ![]() m, kterou
budeme považovat za počáteční polohu (obr. 8).
Potom disk uvolníme. Po dosažení nejnižší polohy začne disk opět
vystupovat nahoru.
m, kterou
budeme považovat za počáteční polohu (obr. 8).
Potom disk uvolníme. Po dosažení nejnižší polohy začne disk opět
vystupovat nahoru.
![]() v průběhu
pohybu disku se trvale nachází pod bodem
v průběhu
pohybu disku se trvale nachází pod bodem ![]() (obr. 8).
(obr. 8).