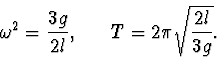![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.1.2 Kmity homogenní tyče
O úroveň výše: 2.1.2 Kmity homogenní tyče
Pokračovat: 2.1.3 Kmity nabité kuličky
Závěsná vlákna svírají s vertikálním směrem úhel 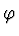 (v rovnovážné poloze je
(v rovnovážné poloze je 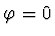 ). Pohyb tyčky je popsán pohybovou
rovnicí
). Pohyb tyčky je popsán pohybovou
rovnicí
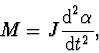 |
(2.1) |
kde 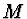 je velikost
momentu vnějších sil,
je velikost
momentu vnějších sil, 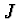 moment setrvačnosti tyčky vzhledem k ose
moment setrvačnosti tyčky vzhledem k ose
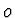 . Označíme-li délku tyčky
. Označíme-li délku tyčky 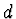 a její hmotnost
a její hmotnost 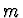 , pak moment
setrvačnosti
, pak moment
setrvačnosti
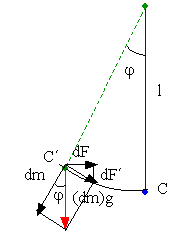
Nyní určíme velikost momentu 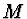 . Otáčivý pohyb způsobují jen složky
tíhové síly působící na tyčku. V rovnovážné poloze se tíhová síla
ruší pevností závěsu. Je-li vlákno vychýleno o úhel
. Otáčivý pohyb způsobují jen složky
tíhové síly působící na tyčku. V rovnovážné poloze se tíhová síla
ruší pevností závěsu. Je-li vlákno vychýleno o úhel 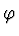 , ruší
se jen složka ve směru závěsu, složka tíhové síly kolmá na závěs udává
otáčivý moment. Element momentu
, ruší
se jen složka ve směru závěsu, složka tíhové síly kolmá na závěs udává
otáčivý moment. Element momentu 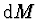 stanovíme podle obr. 3.
stanovíme podle obr. 3.
 |
 |
| Obr. 3 |
Obr. 4 |
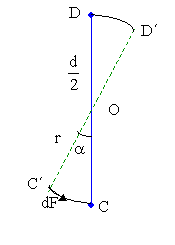
Uvažujeme dva symetricky položené elementy tyčky 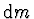 ve
vzdálenosti
ve
vzdálenosti 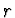 od osy otáčení. Na každý z těchto elementů působí ve
směru kolmém k závěsům stejně velká elementární síla
od osy otáčení. Na každý z těchto elementů působí ve
směru kolmém k závěsům stejně velká elementární síla
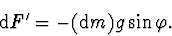 |
(2.2) |
Její průmět do vodorovné roviny je
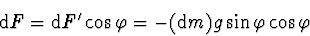 |
(2.3) |
a vytváří dvojici sil o momentu
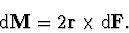 |
(2.4) |
Vektor
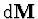 leží v ose
leží v ose 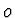 , vektory
, vektory 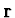 ,
,
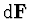 pak leží ve vodorovné rovině. Velikost momentu
pak leží ve vodorovné rovině. Velikost momentu
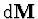 je
je
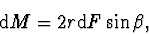 |
(2.5) |
kde 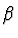 je úhel, který svírají vektory
je úhel, který svírají vektory 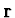 a
a
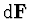 .
Úhel
.
Úhel 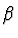 určíme z rovnoramenného trojúhelníku
určíme z rovnoramenného trojúhelníku 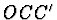 (obr. 4):
(obr. 4):
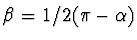 . Dosazením (3) a
. Dosazením (3) a 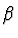 do (5) dostaneme
do (5) dostaneme
kde jsme za 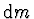 dosadili
dosadili
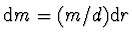 .
.
Protože všechny elementární momenty mají stejný směr, tj. směr osy
 , můžeme je sečíst algebraicky:
, můžeme je sečíst algebraicky:
Při malých výchylkách je
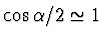 ,
,
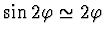 :
:
a jelikož podle obrázku je
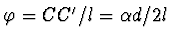 ,
,
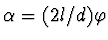 , dostaneme
, dostaneme
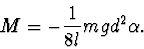 |
(2.6) |
Dosadíme (6) do pohybové rovnice (1), pak po úpravě obdržíme
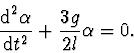 |
(2.7) |
Výsledek: Rovnice (7) je rovnice harmonických kmitů s úhlovou
frekvencí 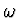 a periodou kmitů
a periodou kmitů 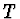 :
:
![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.1.2 Kmity homogenní tyče
O úroveň výše: 2.1.2 Kmity homogenní tyče
Pokračovat: 2.1.3 Kmity nabité kuličky
Milan Šiňor
2000-02-17
![]() (v rovnovážné poloze je
(v rovnovážné poloze je ![]() ). Pohyb tyčky je popsán pohybovou
rovnicí
). Pohyb tyčky je popsán pohybovou
rovnicí
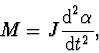


![]() ve
vzdálenosti
ve
vzdálenosti ![]() od osy otáčení. Na každý z těchto elementů působí ve
směru kolmém k závěsům stejně velká elementární síla
od osy otáčení. Na každý z těchto elementů působí ve
směru kolmém k závěsům stejně velká elementární síla
![]() leží v ose
leží v ose ![]() , vektory
, vektory ![]() ,
,
![]() pak leží ve vodorovné rovině. Velikost momentu
pak leží ve vodorovné rovině. Velikost momentu
![]() je
je
![]() , můžeme je sečíst algebraicky:
, můžeme je sečíst algebraicky:
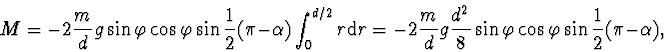
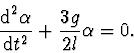
![]() a periodou kmitů
a periodou kmitů ![]() :
: