2.1.2 Kmity homogenní tyče

Zadání: Tenká homogenní tyčka je zavěšena na dvou rovnoběžných vláknech délky $l=120$mm a koná kmitavý pohyb kolem svislé osy procházející jejím těžištěm. Při kmitání zůstává těžiště stále na stejné vertikální přímce. Určete periodu kmitů za předpokladu, že amplituda kmitů je malá.

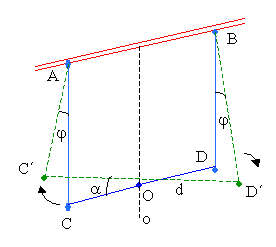
Obr. 2

Návod: Při řešení vycházíme z obr. 2. Při rotačním kmitavém pohybu tyčka prochází různými vodorovnými rovinami. V nejnižší vodorovné rovině se nachází při nulové výchylce, v nejvyšší při maximální výchylce.