1. Dokážeme, že tvrzení platí pro ![]() (obr. 1). Podle zákona lomu
(obr. 1). Podle zákona lomu
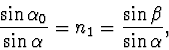
z toho
2. Podle předpokladu z ![]() -té destičky vystupuje paprsek do vakua
pod úhlem
-té destičky vystupuje paprsek do vakua
pod úhlem ![]() (obr. 2), proto
(obr. 2), proto
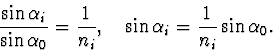 |
(2.63) |
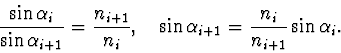 |
(2.64) |
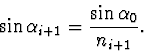 |
(2.65) |
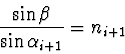
a po dosazení z (3):
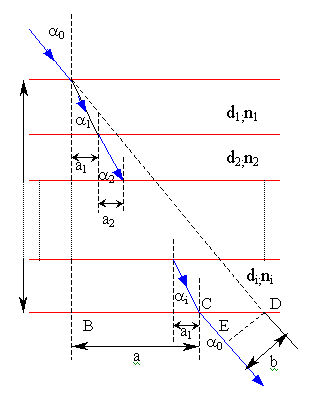 Obr. 3
Obr. 3 |
Pomocí (1) dostaneme
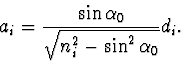
Potom
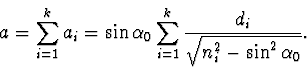 |
(2.66) |
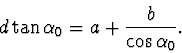
Odtud
![]() a po dosazení ze (4)
a po dosazení ze (4)
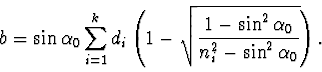
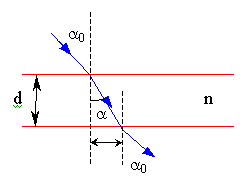 Obr. 4
Obr. 4 |
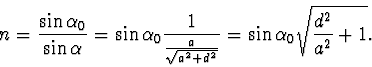
Po dosazení z (4) a úpravě
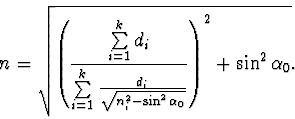
Výsledek: Pro zadané hodnoty:
![]() m,
m,
![]() m,
m, ![]() .
.