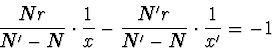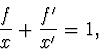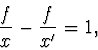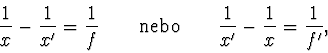![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.5.0.2 Lom kulovou lámavou
O úroveň výše: 2.5.0.2 Lom kulovou lámavou
Pokračovat: 2.5.0.2.2 Zobrazovací rovnice pro
Dvě prostředí o absolutních indexech lomu 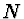 a
a 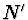 jsou
oddělena částí kulové plochy, tj. kulovým rozhraním. Prostor vlevo od
kulové plochy je skutečný prostor předmětový, vpravo skutečný prostor
obrazový. Každá přímka vedená středem koule může být optickou osou.
Zvolme tuto osu vodorovnou a na ní v prostředí o indexu lomu
jsou
oddělena částí kulové plochy, tj. kulovým rozhraním. Prostor vlevo od
kulové plochy je skutečný prostor předmětový, vpravo skutečný prostor
obrazový. Každá přímka vedená středem koule může být optickou osou.
Zvolme tuto osu vodorovnou a na ní v prostředí o indexu lomu 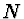 bod
bod
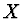 . Tímto bodem veďme paprsek, který svírá s optickou osou úhel
. Tímto bodem veďme paprsek, který svírá s optickou osou úhel
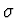 a který dopadá na kulovou plochu v bodě
a který dopadá na kulovou plochu v bodě 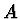 pod úhlem
pod úhlem
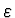 . Zde se paprsek lomí do prostředí s indexem lomu
. Zde se paprsek lomí do prostředí s indexem lomu 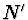 ,
takže s kolmicí k rozhraní v bodě
,
takže s kolmicí k rozhraní v bodě 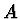 svírá úhel
svírá úhel 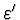 a
optickou osu protíná pod úhlem
a
optickou osu protíná pod úhlem 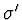 v bodě
v bodě 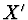 . Úhel
kolmice dopadu vztyčené v bodě dopadu
. Úhel
kolmice dopadu vztyčené v bodě dopadu 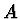 s optickou osou označme
s optickou osou označme 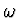 .
.
Označme průsečík optické osy s kulovou plochou, tzv. vrchol plochy,
písmenem 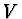 a průsečík kolmice spuštěné z bodu
a průsečík kolmice spuštěné z bodu 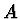 na optickou osu
na optickou osu
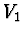 . Je-li úhel
. Je-li úhel 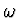 malý, pak můžeme přibližně říci, že
kolmice spuštěná z bodu
malý, pak můžeme přibližně říci, že
kolmice spuštěná z bodu 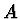 na optickou osu protíná optickou osu
v bodě
na optickou osu protíná optickou osu
v bodě 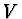 , tj. že body
, tj. že body 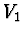 a
a 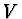 jsou totožné. Označme dále
jsou totožné. Označme dále
Poněvadž 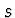 je malé, lze psát
je malé, lze psát
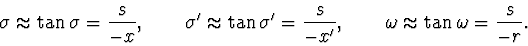 |
(2.47) |
a ze zákona Snellova plyne pro malé úhly
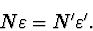 |
(2.48) |
Z 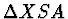 a z
a z 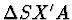 plyne
plyne
a dosazením do (2) dostáváme
a úpravou
Dosazením z (1) vychází
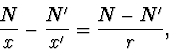 |
(2.49) |
což je zobrazovací rovnice optické soustavy. Známe-li 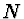 ,
, 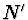 a
a
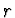 , můžeme ke každému
, můžeme ke každému 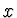 určit příslušné
určit příslušné 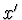 . Tato vzdálenost
nezávisí za uvedeného omezení na úhlu
. Tato vzdálenost
nezávisí za uvedeného omezení na úhlu 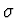 . Bod předmětový
. Bod předmětový 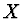 a
bod obrazový
a
bod obrazový 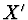 se nazývají sdruženými (konjugovanými)
vzhledem k lámavé ploše.
se nazývají sdruženými (konjugovanými)
vzhledem k lámavé ploše.
Pro předmět v nekonečnu, tj. pro 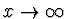 , dostáváme z (3)
, dostáváme z (3)
Tuto vzdálenost nazýváme obrazovou ohniskovou vzdáleností
zobrazovací soustavy a označujeme jí 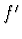 . Jestliže
. Jestliže 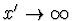 ,
tzn. že obraz má vzniknout v nekonečnu, potom z (3) plyne
,
tzn. že obraz má vzniknout v nekonečnu, potom z (3) plyne
Tuto vzdálenost nazýváme předmětovou ohniskovou vzdáleností
zobrazovací soustavy a označujeme jí 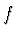 . Platí tedy pro ohniskové
vzdáleností
. Platí tedy pro ohniskové
vzdáleností
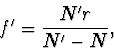 |
(2.50) |
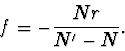 |
(2.51) |
Je-li 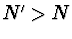 a
a 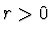 , je
, je 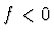 ,
, 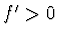 , je-li
, je-li 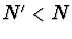 a
a 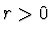 , je
, je 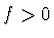 ,
, 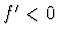 . Tak např. pro korunové sklo (
. Tak např. pro korunové sklo (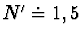 ) vychází
) vychází 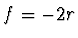 ,
, 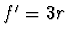 . Naneseme-li na optickou osu
od bodu
. Naneseme-li na optickou osu
od bodu 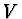 vzdálenost
vzdálenost 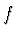 a vzdálenost
a vzdálenost 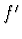 a respektujeme-li
znaménka, dostaneme předmětové ohnisko
a respektujeme-li
znaménka, dostaneme předmětové ohnisko 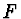 a obrazové ohnisko
a obrazové ohnisko 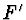 (obr. 5).
(obr. 5).
Násobíme-li zobrazovací rovnici optické soustavy (3) výrazem
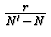 , dostaneme
, dostaneme
a užitím (4) a (5) dostaneme
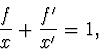 |
(2.52) |
což je upravena zobrazovací rovnice optické soustavy ve tvaru Gaussově.
Zobrazovací rovnici pro čočku, tzv. čočkovou rovnici,
můžeme psát pak ve tvaru
kde 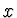 a
a 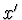 jsou vzdálenosti předmětu, resp. obrazu, měřené od
příslušných kladných hlavních rovin, nebo ve tvaru Newtonově
jsou vzdálenosti předmětu, resp. obrazu, měřené od
příslušných kladných hlavních rovin, nebo ve tvaru Newtonově
Z čočkové rovnice vychází pro čočku:
![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.5.0.2 Lom kulovou lámavou
O úroveň výše: 2.5.0.2 Lom kulovou lámavou
Pokračovat: 2.5.0.2.2 Zobrazovací rovnice pro
Milan Šiňor
2000-02-17
![]() a
a ![]() jsou
oddělena částí kulové plochy, tj. kulovým rozhraním. Prostor vlevo od
kulové plochy je skutečný prostor předmětový, vpravo skutečný prostor
obrazový. Každá přímka vedená středem koule může být optickou osou.
Zvolme tuto osu vodorovnou a na ní v prostředí o indexu lomu
jsou
oddělena částí kulové plochy, tj. kulovým rozhraním. Prostor vlevo od
kulové plochy je skutečný prostor předmětový, vpravo skutečný prostor
obrazový. Každá přímka vedená středem koule může být optickou osou.
Zvolme tuto osu vodorovnou a na ní v prostředí o indexu lomu ![]() bod
bod
![]() . Tímto bodem veďme paprsek, který svírá s optickou osou úhel
. Tímto bodem veďme paprsek, který svírá s optickou osou úhel
![]() a který dopadá na kulovou plochu v bodě
a který dopadá na kulovou plochu v bodě ![]() pod úhlem
pod úhlem
![]() . Zde se paprsek lomí do prostředí s indexem lomu
. Zde se paprsek lomí do prostředí s indexem lomu ![]() ,
takže s kolmicí k rozhraní v bodě
,
takže s kolmicí k rozhraní v bodě ![]() svírá úhel
svírá úhel ![]() a
optickou osu protíná pod úhlem
a
optickou osu protíná pod úhlem ![]() v bodě
v bodě ![]() . Úhel
kolmice dopadu vztyčené v bodě dopadu
. Úhel
kolmice dopadu vztyčené v bodě dopadu ![]() s optickou osou označme
s optickou osou označme ![]() .
.
![]() a průsečík kolmice spuštěné z bodu
a průsečík kolmice spuštěné z bodu ![]() na optickou osu
na optickou osu
![]() . Je-li úhel
. Je-li úhel ![]() malý, pak můžeme přibližně říci, že
kolmice spuštěná z bodu
malý, pak můžeme přibližně říci, že
kolmice spuštěná z bodu ![]() na optickou osu protíná optickou osu
v bodě
na optickou osu protíná optickou osu
v bodě ![]() , tj. že body
, tj. že body ![]() a
a ![]() jsou totožné. Označme dále
jsou totožné. Označme dále
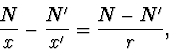
![]() , dostáváme z (3)
, dostáváme z (3)
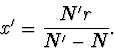
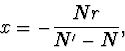
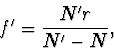
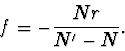
![]() , dostaneme
, dostaneme