2.1.8.1 Řešení

Zpět: 2.1.8 Kmitání 2 těles O úroveň výše: 2.1.8 Kmitání 2 těles Pokračovat: 2.2 Vlny 1

2.1.8.1 Řešení

a)

Souřadnicovou soustavu

umístíme ve směru spojnice těles. Její počátek umístíme do hmotného středu (obr. 10). Pak platí

$\begin{displaymath} m_1x_1+m_2x_2=0 \end{displaymath}$

(2.19)

a dále pro (nulovou) souřadnici hmotného středu

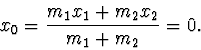
$\begin{displaymath} x_0=\frac{m_1x_1+m_2x_2}{m_1+m_2}=0. \end{displaymath}$

Rovnice (19) platí pro každý okamžik pohybu, jako důsledek zákona zachování hybnosti těles; v každém okamžiku je hybnost izolované soustavy nulová.

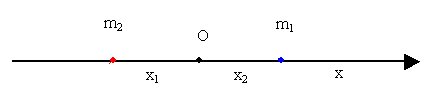Obr. 10

Označíme , souřadnice těles v případě nedeformované pružiny. Podle (19) pro ně rovněž platí

$\begin{displaymath} m_1(x_1)_0+m_2(x_2)_0=0. \end{displaymath}$

(2.20)

Ze vztahů (19) a (20) máme

$\begin{displaymath} m_1\Delta x_1+m_2\Delta x_2=0,~~~~\Delta x_1=x_1-(x_1)_0,~~~~\Delta x_2=x_2-(x_2)_0. \end{displaymath}$

(2.21)

Pro výchylky těles platí

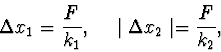$\begin{displaymath} \Delta x_1=\frac{F}{k_1},~~~~\mid \Delta x_2 \mid =\frac{F}{k_2}, \end{displaymath}$

(2.22)

kde

je velikost síly napínající pružinu,

je tuhost části pružiny mezi prvním tělesem a nepohyblivým bodem pružiny,

je tuhost části pružiny mezi druhým tělesem a nepohyblivým bodem pružiny. Síly působí ve směrech opačných k výchylkám.

Pohyb těles je možné modelovat jako jednoduchý kmitavý pohyb dvou těles upevněných na konci pružiny, bod je v klidu.

b)

Z navrženého modelu vyplývá, že v klidu je takový bod pružiny, který její délku v nedeformovaném stavu rozděluje v poměru určeném vztahem

$\begin{displaymath} \frac{m_1}{m_2}=-\frac{(x_2)_0}{(x_1)_0}, ~~~ \mbox{protože}~~ (x_2)_0<0. \end{displaymath}$

Poloha tohoto bodu je totožná s polohou hmotného středu obou těles.

c)

Z (22) a vztahu $F=k(\mid \Delta x_1 \mid + \mid \Delta x_2 \mid)$ máme

$\begin{displaymath} k_1\mid \Delta x_1\mid +k_2\mid \Delta x_2 \mid = k(\mid \Delta x_1 \mid + \mid \Delta x_2 \mid). \end{displaymath}$

(2.23)

Obě tělesa konají jednoduchý kmitavý pohyb, trvale s opačnou fází, protože pro jejich rychlosti ${\bf v}_1$ , ${\bf v}_2$ platí

$\begin{displaymath} {\bf v}_1=-\frac{m_2}{m_1}{\bf v}_2. \end{displaymath}$

Doby kmitů těles

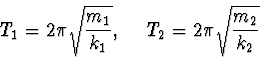
$\begin{displaymath} T_1=2\pi \sqrt{\frac{m_1}{k_1}},~~~~T_2=2\pi\sqrt{\frac{m_2}{k_2}} \end{displaymath}$

určíme pomocí (21) a (23), neboť

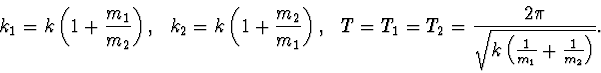$\begin{displaymath} k_1=k\left(1+\frac{m_1}{m_2}\right),~~~ k_2=k\left(1+ \frac{... ...rac{2\pi}{\sqrt{k\left( \frac{1}{m_1}+ \frac{1}{m_2}\right)}}. \end{displaymath}$

(2.24)

d)

V případě, že $m_2\gg m_1$ , vyplývá ze (24)

$\begin{displaymath} T'=2\pi \sqrt{\frac{m_1}{k}}. \end{displaymath}$

Druhé těleso je přibližně v klidu, harmonické kmity koná pouze první těleso.

Výsledek: $T\simeq 0,40$ s, $T'\simeq 0,44$ s.

Zpět: 2.1.8 Kmitání 2 těles O úroveň výše: 2.1.8 Kmitání 2 těles Pokračovat: 2.2 Vlny 1

Milan Šiňor
2000-02-17