![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.7.20 Konečná jáma **
O úroveň výše: 2.7.20 Konečná jáma **
Pokračovat: 2.7.21 Konečná potenciálová bariera
Průběh potenciálové jámy je možné napsat ve tvaru: 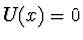 pro
pro
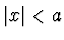 ,
, 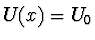 pro
pro
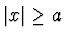 .
Řešení tohoto problému si proto rozdělíme na řešení Schrödingerovy
rovnice pro obě uvedené oblasti. V případě, kdy
.
Řešení tohoto problému si proto rozdělíme na řešení Schrödingerovy
rovnice pro obě uvedené oblasti. V případě, kdy
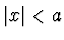 je obecné řešení
je obecné řešení
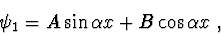 |
(2.93) |
kde
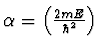 . Nyní se omezíme na řešení této rovnice v intervalu
. Nyní se omezíme na řešení této rovnice v intervalu
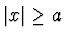 , která ma tvar
, která ma tvar
Obecné řešení této rovnice pro případ 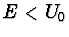 (vázane stavy) je
dáno výrazem
(vázane stavy) je
dáno výrazem
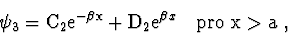 |
(2.94) |
kde
![$\beta = \left[ {\frac{{2m(U_0 - E)}}{{\hbar ^2 }}}
\right]^{1/2}$](img1069.gif) . Vzhledem k hraničním podmínkám pro
. Vzhledem k hraničním podmínkám pro
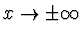 (kdy vlnová funkce musí konvergovat k nule) je třeba, aby v oblasti
(kdy vlnová funkce musí konvergovat k nule) je třeba, aby v oblasti
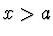 bylo v obecném řešení (2.94)
bylo v obecném řešení (2.94) 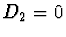 a v oblasti
a v oblasti
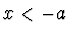 bylo
bylo 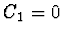 . Tím řešení (2.94) dostaneme ve
tvaru
. Tím řešení (2.94) dostaneme ve
tvaru
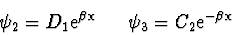 |
(2.95) |
V důsledku spojitosti vlnové funkce a její první derivace v celém
prostoru, musí v bodech 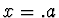 platit
platit
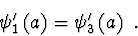 |
(2.96) |
Tím po dosazení z (2.93) a (2.94) dostaneme
pro koeficienty 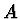 ,
, 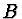 ,
, 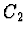 a
a 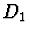 soustavu čtyř lineárních
homogenních rovnic
soustavu čtyř lineárních
homogenních rovnic
Aby tato soustava měla řešení, musí determinant soustavy být roven nule
Jestliže tuto kvadratickou rovnici rozřešíme vzhledem k 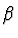 ,
dostaneme dvě podmínky pro řešení rovnic (2.96)
,
dostaneme dvě podmínky pro řešení rovnic (2.96)
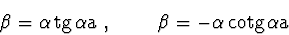 |
(2.97) |
Obě tyto podmínky však nelze splnit současně a proto můžeme obecné
řešení rovnic (2.96) rozdělit na dvě třídy řešení. První
třída platí pro
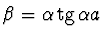 . Po dosazení za
. Po dosazení za
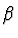 do (4) dostaneme
do (4) dostaneme
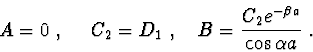 |
(2.98) |
Druhá třída patí pro
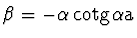
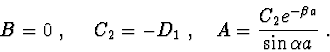 |
(2.99) |
Energetické hladiny částice určíme numerickým nebo grafickým řešením
rovnic (2.97). Proto si ukážeme jednoduchou grafickou
metodu jak lze energetické hladiny určit. Položme 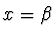 ,
, 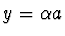 . Potom rovnice (2.97) dostávají tvar
. Potom rovnice (2.97) dostávají tvar
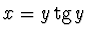 a
a
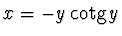 , přitom však veličiny
, přitom však veličiny 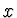 ,
,
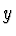 splňují rovnost
splňují rovnost
Vzhledem k tomu, že 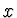 ,
, 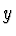 mohou nabývat pouze kladných hodnot,
úroveň energie částice určují body (ležící v prvém kvadrantu), ve
kterých se protíná křivka
mohou nabývat pouze kladných hodnot,
úroveň energie částice určují body (ležící v prvém kvadrantu), ve
kterých se protíná křivka
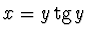 (nebo
(nebo
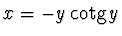 ) s kružnicí
) s kružnicí
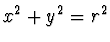 , kde
, kde
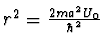 . Tím máme určeny energetické hladiny
příslušné dané vlnové funkci (tj. ve stavu částice), která pro případ
prvé třídy řešení je vzhledem k (2.93), (2.95)
a (2.98) rovna
. Tím máme určeny energetické hladiny
příslušné dané vlnové funkci (tj. ve stavu částice), která pro případ
prvé třídy řešení je vzhledem k (2.93), (2.95)
a (2.98) rovna
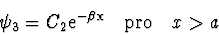 |
(2.100) |
a pro případ druhé třídy řešení má tvar
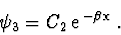 |
(2.101) |
Aby řešení dané úlohy bylo úplné, je nutné určit koeficient 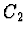 z normovací podmínky. Pro první případ vzhledem k (2.100) dostaneme
z normovací podmínky. Pro první případ vzhledem k (2.100) dostaneme
Jestliže nyní využijeme vztahu
 ,
dostaneme již konečný výraz pro koeficient
,
dostaneme již konečný výraz pro koeficient 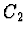
![\begin{displaymath}{
}
\frac{1}{{\left\vert {C_2 } \right\vert^2 }} = ae^{ - 2\b...
...^2 }}{{\alpha ^2 }} + \frac{\beta }{{\alpha ^2 a}}} \right]\ .
\end{displaymath}](img1107.gif) |
(2.102) |
Analogickým způsobem můžeme určit koeficient 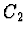 i pro druhé řešení
dané vztahy (2.101). Hledaný koeficient
i pro druhé řešení
dané vztahy (2.101). Hledaný koeficient 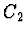 je však opět
dán výrazem (2.102).
je však opět
dán výrazem (2.102).
![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.7.20 Konečná jáma **
O úroveň výše: 2.7.20 Konečná jáma **
Pokračovat: 2.7.21 Konečná potenciálová bariera
Milan Šiňor
2000-02-17
![]() pro
pro
![]() ,
, ![]() pro
pro
![]() .
Řešení tohoto problému si proto rozdělíme na řešení Schrödingerovy
rovnice pro obě uvedené oblasti. V případě, kdy
.
Řešení tohoto problému si proto rozdělíme na řešení Schrödingerovy
rovnice pro obě uvedené oblasti. V případě, kdy
![]() je obecné řešení
je obecné řešení
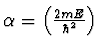 . Nyní se omezíme na řešení této rovnice v intervalu
. Nyní se omezíme na řešení této rovnice v intervalu
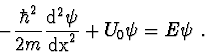
![$\beta = \left[ {\frac{{2m(U_0 - E)}}{{\hbar ^2 }}}
\right]^{1/2}$](img1069.gif) . Vzhledem k hraničním podmínkám pro
. Vzhledem k hraničním podmínkám pro
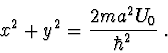
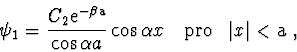
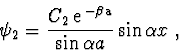
![\begin{displaymath}
\begin{array}{l}
\int\limits_{ - \infty }^{ + \infty } {\le...
...}{\alpha }\,{\rm tg}\,\alpha a} \right] = 1\ . \\
\end{array}\end{displaymath}](img1106.gif)