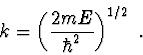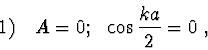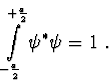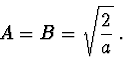![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.7.19 Nekonečná potenciálová jáma
O úroveň výše: 2.7.19 Nekonečná potenciálová jáma
Pokračovat: 2.7.20 Konečná jáma **
Vzhledem k tomu, že stěny jámy jsou ideálně nepropustné, částice se
může vyskytovat pouze uvnitř intervalu
Vně tohoto intervalu je tudíž vlnová funkce rovna nule. Pro vlnovou
funkci proto musí platit hraniční podmínky
Při hledání energetických hladin a vlnových funkcí částice, která se
nachází uvnitř jámy vyjdeme z amplitudové Schrödingerovy rovnice,
která má v intervalu
tvar
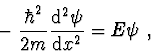 |
(2.87) |
kde 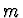 je hmotnost částice.
Obecné řešení rovnice (2.87) je rovno
je hmotnost částice.
Obecné řešení rovnice (2.87) je rovno
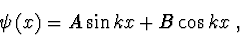 |
(2.88) |
kde
Vzhledem k hraničním podmínkám musí platit
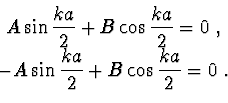 |
(2.89) |
Řešením těchto rovnic, které musí platit současně dostáváme dvě třídy řešení
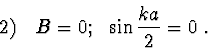 |
(2.90) |
Řešení rovnice pro 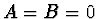 nemá fyzikální význam, neboť vlnová
funkce je v tomto případě rovna nule v celém prostoru. Pro obě třídy
musí platit
nemá fyzikální význam, neboť vlnová
funkce je v tomto případě rovna nule v celém prostoru. Pro obě třídy
musí platit
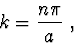 |
(2.91) |
kde 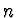 je celé liché číslo pro třídu řešení 1) a celé sudé číslo pro
třídu 2). Vlnové funkce a odpovídající energetické hladiny dostaneme
dosazením (2.90) a (2.91) do obecného řešení
(2.88). Tím obě třídy řešení dostaneme ve tvaru
je celé liché číslo pro třídu řešení 1) a celé sudé číslo pro
třídu 2). Vlnové funkce a odpovídající energetické hladiny dostaneme
dosazením (2.90) a (2.91) do obecného řešení
(2.88). Tím obě třídy řešení dostaneme ve tvaru
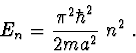 |
(2.92) |
Řešení pro 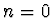 nemá fyzikální význam, neboť vlnová funkce je rovna
nule v celém prostoru. Obdobně případ, kdy
nemá fyzikální význam, neboť vlnová funkce je rovna
nule v celém prostoru. Obdobně případ, kdy 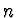 je záporné celé číslo,
nedává fyzikálně nová řešení, neboť řešení se záporným a kladným
je záporné celé číslo,
nedává fyzikálně nová řešení, neboť řešení se záporným a kladným 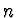 jsou lineárně závislá. Konstanty
jsou lineárně závislá. Konstanty 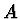 a
a 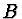 určíme z normovací
podmínky
určíme z normovací
podmínky
Po dosazení z (2.92) dostaneme
Nyní již máme celý problém vyřešen. Jako řešení jsme dostali
nekonečnou množinu diskrétních hladin energie, které odpovídají všem
kladným kvantovým číslům 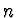 . Ke každé energetické hladině přísluší
jediná vlnová funkce daná vztahem (2.92).
. Ke každé energetické hladině přísluší
jediná vlnová funkce daná vztahem (2.92).
![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.7.19 Nekonečná potenciálová jáma
O úroveň výše: 2.7.19 Nekonečná potenciálová jáma
Pokračovat: 2.7.20 Konečná jáma **
Milan Šiňor
2000-02-17