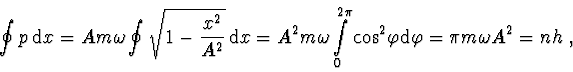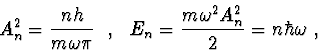![[*]](icons/DocsLeftArrow2.gif)
![[*]](icons/DocsUpArrow2.gif)
![[*]](icons/DocsContents2.gif)
![[*]](icons/DocsRightArrow2.gif)
Zpět: 2.7.18 Harmonický oscilátor (energetické
O úroveň výše: 2.7.18 Harmonický oscilátor (energetické
Pokračovat: 2.7.19 Nekonečná potenciálová jáma
Konzervativní síla
která na částici o hmotnosti 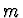 působí, je charakterizována
potenciální energií
působí, je charakterizována
potenciální energií
Vzhledem k tomu, že celková energie částice je prvním integrálem
pohybu, dostaneme
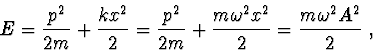 |
(2.86) |
kde
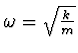 je úhlová frekvence kmitů
oscilátoru a
je úhlová frekvence kmitů
oscilátoru a 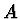 je jejich amplituda. Ze vztahu (2.86)
určíme hybnost
je jejich amplituda. Ze vztahu (2.86)
určíme hybnost
Použitím Bohrovy-Sommerfeldovy podmínky za předpokladu
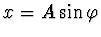 dostaneme
dostaneme
z čehož pro amplitudy 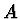 a energie podle (2.86) plyne vztah
a energie podle (2.86) plyne vztah
kde
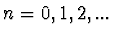
Milan Šiňor
2000-02-17
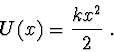
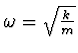 je úhlová frekvence kmitů
oscilátoru a
je úhlová frekvence kmitů
oscilátoru a