Zahřejeme-li krystalickou látku, dojde ke změně jejích rozměrů. Uvažujeme-li pouze jeden krystalek, pak koeficient tepelné roztažnosti bude nabývat různých hodnot podle toho, ke které soustavě krystalek patří. V případě kubických krystalů nabývá pouze jedné hodnoty, což znamená, že v libovolném směru (směr hrany krychle, směr stěnové nebo tělesové úhlopříčky) se látka s kubickou elementární buňkou roztahuje stejně.
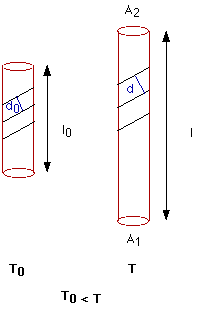
Uvažujme pro jednoduchost vzorek z materiálu s kubickou symetrií ve tvaru tyčky, jejíž délku označíme l0(obr 6.2).

Lineární koeficient tepelné roztažnosti a je definován vztahem
| , |
kde l0 je počáteční délka tyčky, a l délka po zahřátí z počáteční teploty T0 na teplotu T.
Všimněme si, že délka tyčky l je dána vzdáleností dvou bočních ploch A1 a A2. Pak ale můžeme zvolit vzdálenost dvou jiných ploch, která bude měřítkem změny délky. K tomu nám poslouží vzdálenost dvou sousedních krystalových rovin. Z difrakčního diagramu před zahřátím a po zahřátí určíme změnu mezirovinné vzdálenosti
a pomocí Braggovy rovnice vypočítáme
| . |
Z teplotní závislosti difrakčního úhlu q (T ) určíme hodnotu koeficientu teplotní roztažnosti a.
Využití difrakce rentgenového záření v materiálovém výzkumu