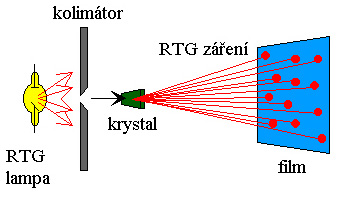
Objev difrakce rentgenových paprsků na krystalové mřížce se svým významem řadí mezi největší úspěchy přírodních věd našeho století. V roce 1913 Max von Laue vyslovil domněnku, že pravidelné uspořádání atomů v krystalech může hrát úlohu trojrozměrné difrakční mřížky. Pozdější experimenty tuto předpověď potvrdily. Ukázaly, že rentgenové paprsky po průchodu nebo po odrazu na krystalu dávají vznik difrakčnímu obrazu s charakterisickými maximy a minimy intenzity difrakčních skvrn. Na obr. 4.1 je jednoduché schéma uspořádání takového experimentu.

Z rentgenové lampy po průchodu kolimátorem dopadá svazek rentgenového záření na krystal. Paprsky difraktované krystalem dopadají na fotografický film. Po vyvolání se na filmu nacházejí uspořádané difrakční stopy (Laueogram) odpovídající pravidelnému rozmístění atomů v krystalu.
Za necelý rok po Laueově objevu ukázal W. H. Bragg se svým synem W. L. Braggem, jak lze z difrakčních obrazů určit souměrnost krystalu, vzájemnou polohu stavebních částic (atomů, iontů) i jejich vzdálenosti v krystalových mřížkách. Z analýzy intenzity difrakčních skvrn na filmech dospěli k závěru, že krystal se chová tak, jako by obsahoval velké množství rovin umístěných jedna za druhou v určitých vzdálenostech . Na obr. 4.2 jsou znázorněny dvě soustavy rovin s různými mezirovinnými vzdálenostmi:
![]()
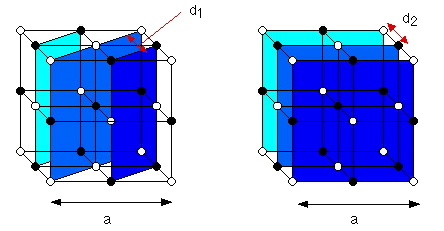
| a) | b) |
Každá rovina rozptýlí jen malé množství záření, avšak výsledný rozptyl od velkého počtu rovin poskytuje intenzitu dostatečnou pro pozorování. Vyberme dvě libovolné paralelní roviny vzdálené o d a nechme na tyto roviny dopadat svazek rovnoběžných rentgenových paprsků (obr. 4.3).
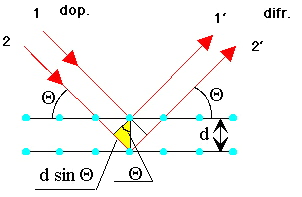
Jak víme z difrakce na mřížce, interferenční maximum difraktovaných paprsků nastává v případě, že jejich dráhový rozdíl je roven celistvému násobku vlnové délky dopadajícího záření. Dráhový rozdíl paprsků 11' a 22' je roven 2dsinq, kde úhel q je úhel, který svírá dopadající paprsek s rovinou krystalu. Podmínka pro vznik difrakčních maxim paprsků 1' a 2' je dána vztahem
| 2dsinq=nl | n=1,2,3.... | . |