Interakce částice s bariérou, tunelový jev

  

Obrázek 7.14: Interakce částice s bariérou, tunelový jev.

V klasické fyzice není z principielních důvodů daných zákonem zachování energie možné, aby částice s kinetickou energií menší než je výška potenciálové bariéry, s níž interaguje, tuto přehradu překonala - může (přesněji řečeno musí) se od ní pouze odrazit. V kvantově mechanickém popisu je situace obecně jiná. Částice má i v případě, že její energie není z klasického pohledu pro průchod bariérou postačující, jistou pravděpodobnost, že bariéru překoná - existuje tzv. tunelový efekt. 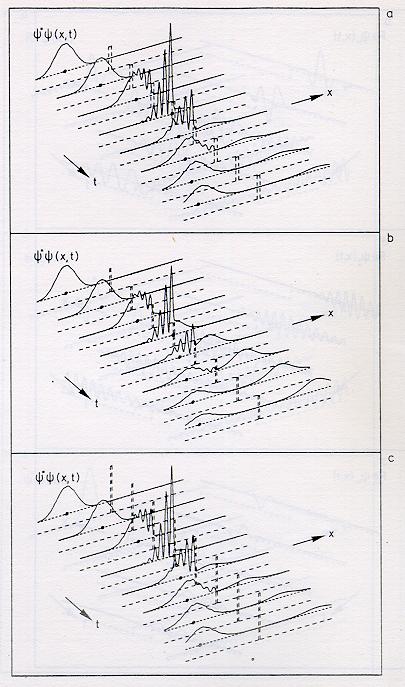Naopak, částice s energií větší než je výška bariéry tuto bariéru obecně překonat nemusí. Obrázek ilustruje situaci při interakci částice, reprezentované vlnovým balíkem gaussovského tvaru, s pravoúhlou bariérou různé výšky a šířky. Částice přichází zleva, kroužky označují polohu klasické částice dopadající na stejnou přehradu. Jestliže v obrázku a) je výška bariéry $V$ a šířka $d$, na obrázku b) je uvažována přehrada o výšce rovněž $V$, ale o šířce $d/2$ a obrázek c) zobrazuje situaci pro hodnoty $2V$ a $d/2$.

Kredit: S. Brandt, H.D. Dahmen: Kvantová mechanika v obrazoch. Vydavatelstvo Alfa, Bratislava 1990

Zpět: Interakce laserového záření s látkou O úroveň výše: Úvodní poznámky Pokračovat: Interference částice na dvou